PLS Progetto Archimede

Sapienza, Università di Roma

DAL CUBO AL CUBO TRONCO

Francesco Di Tommaso – Alessandro Mortellaro – Pietro Scala

I.T.I.S. Galileo Galilei, IV A, IV L

(Nell’ambito del progetto Matematica creativa)

Alcuni solidi archimedei possono essere ottenuti dai solidi platonici troncandone i vertici.

Mostriamo come troncare i vertici di un cubo con il software Cabri 3D.

Prima parte. Costruzione di un cubo.

· Apri Cabri 3D

· Aggiungi alla scena un cubo. Per farlo, vai nella barra degli strumenti. Clicca sulla freccetta sulla penultima icona e seleziona la voce cubo.

· Cabri chiederà su quale piano rappresentare una delle facce del cubo. Una volta scelto il piano, scegli il centro della faccia e uno degli spigoli.

· Dovresti ritrovarti in questa situazione:

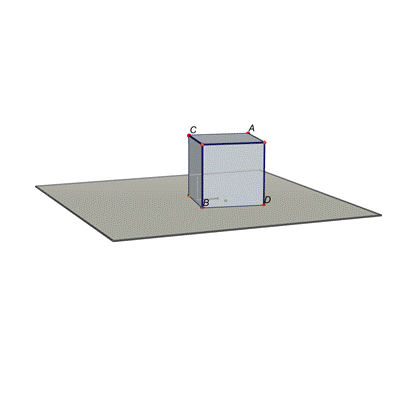
A questo punto clicca con il pulsante destro del mouse sul piano. Comparirà un menù. L’ultima voce è “mostra/nascondi”. Cliccaci sopra e vedrai sparire il piano. Ripeti l’operazione anche con gli assi cartesiani in modo da avere solamente il tuo cubo.

Iniziamo quindi il procedimento per tagliare i vertici.

Per far ciò è necessario determinare il centro del cubo.

Seconda parte. Determinazione del centro del cubo.

· Creiamo due diagonali del cubo. Il comando retta si trova sempre nella barra degli strumenti, è la terza icona da sinistra.

· Trova il punto di intersezione tra le due diagonali premendo la freccia nell’icona del comando punto. Ti si apre quindi un menù a tendina con due voci: punto e punto di intersezione.

Seleziona la seconda voce e seleziona le due rette.

· Comparirà un punto al centro del cubo che chiamiamo O.

· A questo punto nascondi le rette che hai usato per trovare il centro.

Terza parte. Troncamento dei vertici.

· Crea il punto medio M dello spigolo AB.

· Crea il segmento AM.

· Crea un punto P appartenente al segmento AM.

· Crea quindi una sfera (che trovi nel menù a tendina cliccando due volte sull’icona del piano nella barra degli strumenti) di centro O e passante per P.

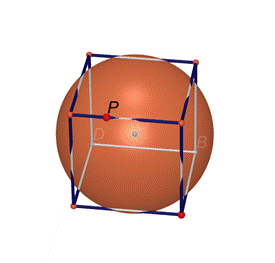
· Trova quindi i punti di intersezione tra la sfera e il cubo usando lo stesso comando che hai usato per il punto di intersezione tra le rette.

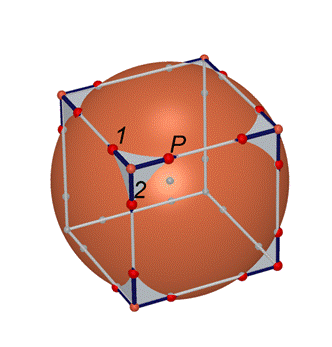
· Nascondi la sfera. Crea quindi un piano passante per i punti 1,2 e P.

· Seleziona poi il comando “seziona poliedro” che trovi cliccando due volte sul comando tetraedro. Una volta cliccato scegli il piano appena creato e poi il cubo. Vedrai che una parte del cubo sparisce.

· Ripeti l’operazione su tutti i gruppi di vertici come quello evidenziato sopra. Arriverai a questo punto.

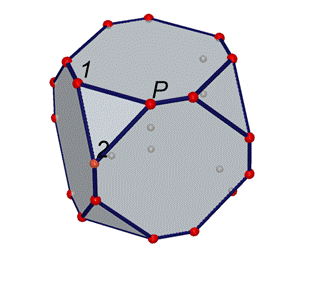
· Ti trovi di fronte ad un poliedro che ha come facce triangoli e ottagoni.

Muovendo il punto P sul segmento AM si vede come varia il poliedro al variare del punto P.

Aprendo il file Cubo_con_vertici_troncati costruito con Cabri 3D si vede chiaramente come varia il poliedro. Per far ciò, una volta aperta la figura, devi muovere con il mouse il punto rosso.

Tuttavia per arrivare veramente ad un solido archimedeo manca ancora qualcosa. Sappiamo che le facce dei poliedri archimedei sono poligoni regolari.

Quindi i nostri triangoli e i nostri ottagoni devono essere regolari, ovvero avere tutti i lati e gli angoli uguali. Come puoi ben notare nella figura precedente, l’ottagono non è certo regolare.

Quindi il nostro prossimo obiettivo sarà innanzitutto dimostrare che i triangoli sono regolari, cioè equilateri, e in seguito trovare un punto E dove posizionare il nostro punto P per avere degli ottagoni regolari.

Quarta parte – Dimostrare che i triangoli sono equilateri

Bisogna a questo punto aprire un piccolo discorso sulle simmetrie. Servirà a capire meglio come dimostreremo la regolarità dei triangoli.

Prendiamo in considerazione un cubo

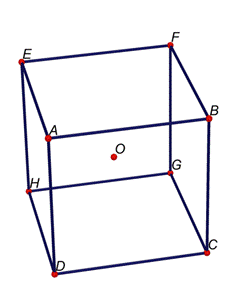
Crea il piano passante per A, D e G, e quindi passante anche per O e F.

Chiamiamo il piano a.

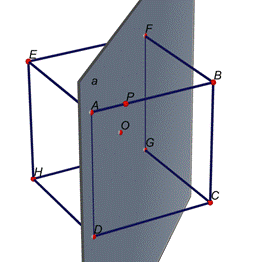
I simmetrici dei punti B e C rispetto al piano a sono E ed H. I simmetrici, invece, di ADFG sono invece gli stessi punti ADFG poiché appartengono al piano di simmetria.

La distanza tra A e B è la stessa tra A ed E. Questo perché i punti B ed E sono tra loro simmetrici. Si trovano alla stessa distanza da A, poiché questo appartiene al piano di simmetria.

Scopriamo quindi che i punti EAB formano un triangolo rettangolo. La lunghezza del segmento EB, ovvero l’ipotenusa del triangolo, si trova facilmente con il teorema di Pitagora.

Analogamente ripetiamo la procedura con il punto P, il cui simmetrico rispetto al piano a è il punto P’.

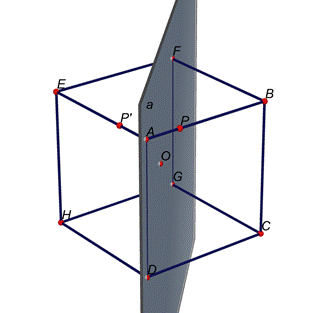
Per quanto detto prima, la distanza tra P e A è la stessa tra P’ ed A. Quindi PP’A formano un triangolo rettangolo la cui ipotenusa è il segmento PP’, facilmente calcolabile con il teorema di Pitagora.

Inoltre per il discorso delle simmetrie, la distanza tra P ed O e tra P’ ed O è la stessa.

Creiamo ora un piano passante per AEC, che chiamiamo b.

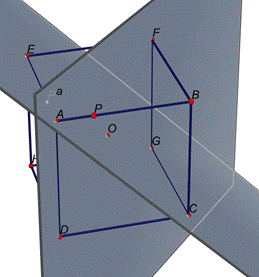
Troviamo il simmetrico di P rispetto al piano b. Chiamiamo questo nuovo punto P^’’, appartenente allo spigolo AD.

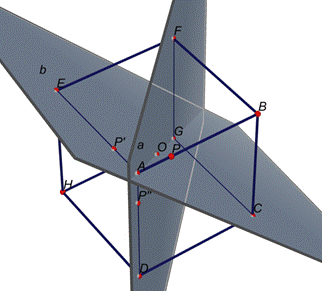
Quindi, per il discorso fatto all’inizio, la distanza tra P ed A è la stessa tra P^’’ ed A, quindi PP^’’A formano un triangolo rettangolo la cui ipotenusa PP^’’ è facilmente calcolabile con Pitagora.

Se la distanza tra P ed A è la stessa tra P’ ed A, e quindi uguale alla distanza tra P^’’ ed A, i punti PP’P^’’ ed A formano tre triangoli rettangoli, PAP’ e PAP^’’ P’AP^’’, i cui cateti sono tutti uguali tra loro e le ipotenuse

PP’ (segmento blu)

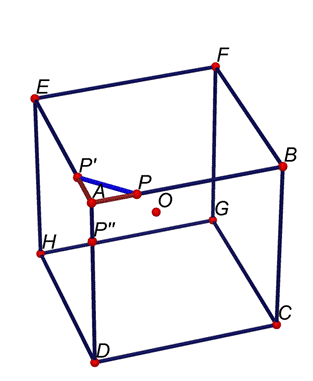
PP^’’ (segmento verde)

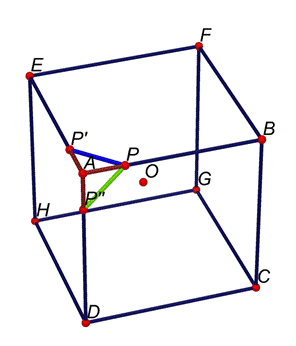
P^’’P’ (segmento rosa)

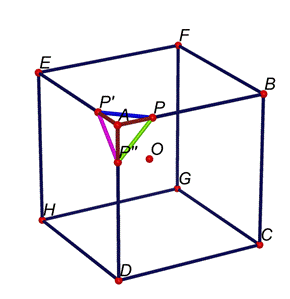
Sono uguali tra loro. Pertanto il triangolo PP’P^’’ è equilatero.

Ricordiamo che P’ è il simmetrico di P rispetto al piano a. Dal momento che il punto O appartiene a questo piano, la distanza tra P ed O è uguale alla distanza tra P’ ed O.

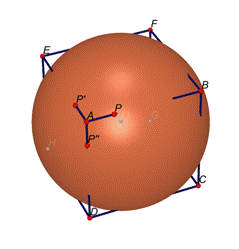
Quindi, se creiamo la sfera di centro O e passante per , il punto P’ può essere considerato come l’intersezione tra la sfera s e il segmento AE. Analogamente il punto P^’’ essere considerato come l’intersezione tra la sfera s e il segmento AB.

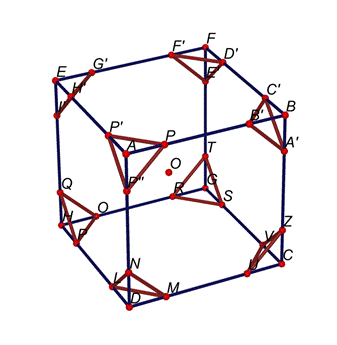
In modo analogo si possono ottenere tutti gli altri vertici dei triangoli intorno ai singoli vertici del cubo.

Parte quinta – Costruire un ottagono regolare avente quattro lati sugli spigoli della faccia ABCD del cubo.

Primo metodo

Tracciare le diagonali del quadrato Q di vertici A, B, C e D. Indichiamo con O la loro intersezione. E’ il centro del quadrato Q.

Disegnare la circonferenza di centro O passante per A. E’ la circonferenza circoscritta al quadrato Q.

Disegnare con il comando “Punto Medio” i punti medi M, M’, M’’, M’’’ dei lati del quadrato Q come in figura.

Tracciare la retta passante per M e M’’ e la retta passante M’ e M’’’.

Indicare con A’, B’, C’ e D’ le intersezioni di queste ultime due rette con la circonferenza circoscritta al quadrato Q come in figura.

Si ha che A’B’C’D’ è un quadrato Q’ di centro O.

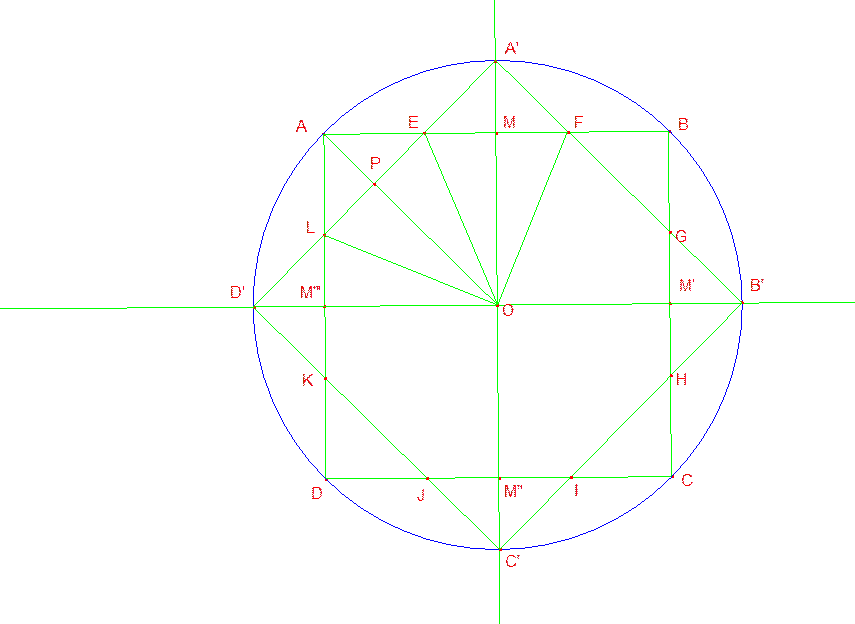
Considerare i punti F, G, H, I, J, K, L di intersezione dei lati dei quadrati Q e Q’ come in figura.

L’ottagono FGHIJKL è l’ottagono regolare cercato avente quattro lati sui lati del quadrato Q.

Secondo metodo.

Tracciare le diagonali del quadrato Q di vertici A, B, C e D. Indichiamo con O la loro intersezione. E’ il centro del quadrato Q.

Disegnare con il comando “Punto Medio” i punti medi M, M’, M’’, M’’’ dei lati del quadrato Q come in figura.

Disegnare la circonferenza di centro O passante per M. Essa è la circonferenza inscritta nel quadrato Q.

Disegnare i quattro punti di intersezione T, T’, T’’ e T’’’ di quest’ultima circonferenza con le diagonali del quadrato e tracciare le quattro rette tangenti alla circonferenza nei punti T, T’, T’’ e T’’’.

Ma come disegnare, per esempio, la retta passante per T’’’ e tangente alla circonferenza?

Si seleziona il comando “perpendicolare”, tenendo premuto il tasto CTRL si seleziona la faccia ABCD, si seleziona poi il punto T’’’ e la retta passante per A e C.

In tal modo abbiamo chiesto di tracciare la retta del piano contenente la faccia ABCD che passi per T’’’ e sia perpendicolare alla retta passante per A e C.

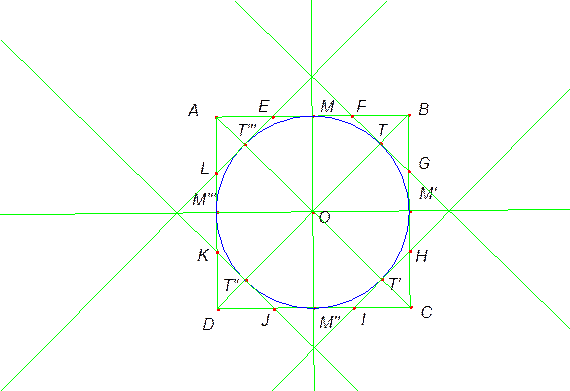
Disegnare i punti F, G, H, I, J, K, L di intersezione delle quattro tangenti con i lati del quadrato Q come in figura.

L’ottagono FGHIJKL è l’ottagono regolare cercato avente quattro lati sui lati del quadrato Q.