PLS Progetto Archimede

Sapienza, Università di Roma

 

 

 

I. T. I. S. Galileo Galilei Roma

DAL CUBO AL ROMBICUBOTTAEDRO PER MEZZO DI UN’ESPANSIONE

 

 

Tudorache Alexandru

I.T.I.S. Galileo Galilei III L

(Nell’ ambito del progetto Matematica Creativa)

 

 

 

 

 

Espansione del cubo

 

·         Cominciamo a disegnare un cubo con il comando predefinito di Cabri 3D.

·         Nascondiamo il piano fondamentale predefinito di Cabri 3D con il comando "mostra/nascosto".

·         Selezioniamo il cubo e scegliamo il comando "stile" della superficie “vuoto”.

·         Prendiamo il comando "punto" si disegna un punto in ogni vertice del cubo e assegniamo una lettera a ciascun punto inserendola dalla tastiera.

·         Indichiamo con l la misura del lato del cubo.

 

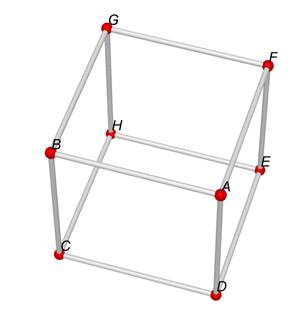
Figura 1

 

·         Prendiamo il vertice B e il vertice E è con il comando "retta" si traccia una retta r1 passante per B ed E.

·         Prendiamo il punto D e il punto G e, con il comando "retta", si traccia la retta r2.

·         Disegniamo il punto O di intersezione delle due rette: è il centro del cubo.

 

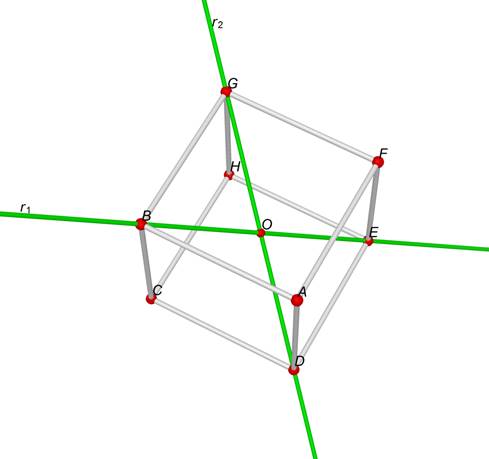
Figura 2

 

 

·         Selezioniamo le due rette costruite in precedenza e con il comando "mostra/nascosto" le nascondiamo lasciando solamente il punto O di intersezione tra le rette. 

·         Con il comando "retta" disegniamo la retta r3 per lo spigolo , la retta r4 per lo spigolo  e la retta r5 per lo spigolo . 

·         Consideriamo ora la semiretta s contenuta nella retta r5, avente l’origine in A e non passante per D, per far ciò consideriamo il punto D’, simmetrico di D rispetto ad A. Consideriamo ora la semiretta s di origine A passante per D’.  

·         Con il comando "punto" (mobile) selezioniamo un punto P sulla semiretta s.

·         Nascondiamo poi il punto D’.

 

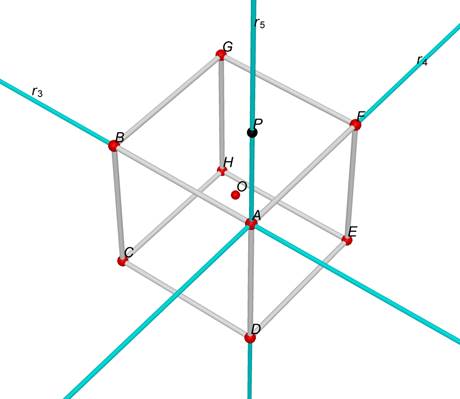
Figura 3

 

·         Disegniamo con il comando "sfera" la sfera di centro O e passante per P.

·         Troviamo tutti i punti di intersezione con le rette ,r3, r4 e r5 secanti la sfera, con il comando "punti di intersezione".

·         Indichiamo i punti secanti la sfera che ne derivano con le lettere I,J,K,L,M,P.

 

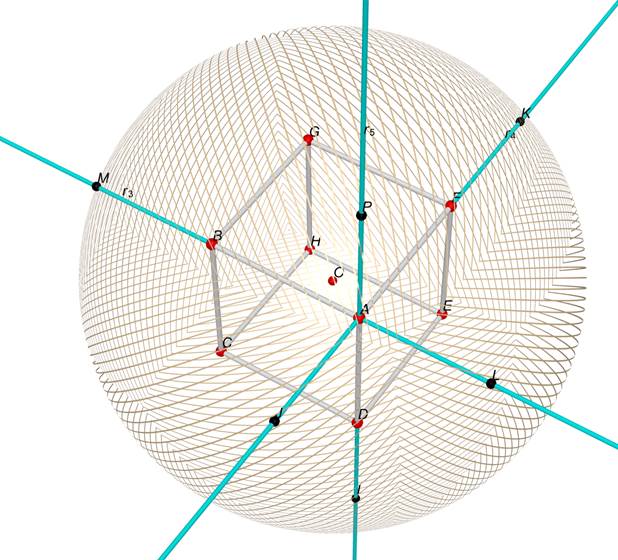
Figura 4

 

·         Nascondiamo la sfera costruita in precedenza lasciando solamente i punti I,J,K,L,M,P.

·         Utilizzando il comando “poligono di n punti” tracciamo il quadrato ABGF.

·         Con il comando “traslazione trasliamo il quadrato ABGF in modo tale che il vertice A sia traslato nel punto P. Otteniamo il quadrato PNQR.

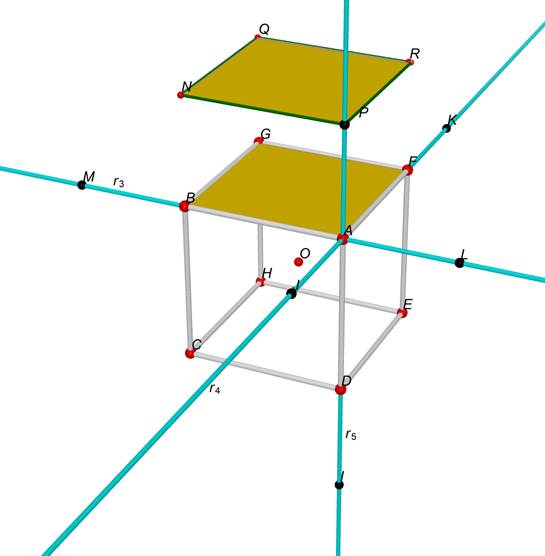
Figura 5

 

Vogliamo in traslare in maniera analoga la faccia CDEH. Osserviamo che il simmetrico del quadrato ABGF rispetto alla simmetria centrale di cento O è il quadrato CDEH. 

·         Pertanto selezioniamo il quadrato PNQR e ne facciamo la simmetria centrale rispetto al punto O ricavando il quadrato ISTU.

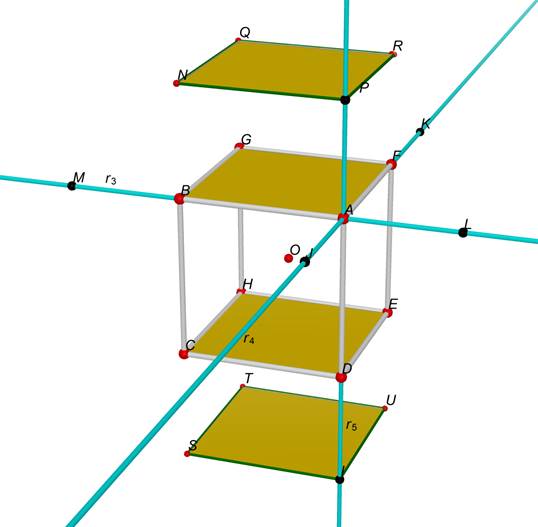
Figura 6

 

 

 In modo analogo possiamo fare l'espansione delle altre facce del cubo.

 

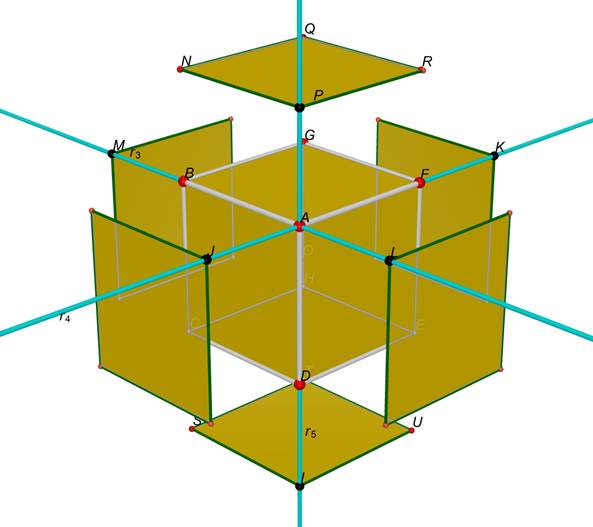
Figura 7

 

 

·         Notiamo che i punti P, J, L sono ottenuti a partire dal vertice A del cubo iniziale.

·         Usando il comando ”triangolo”  disegniamo il triangolo PJL.

·         Disegniamo in modo analogo gli altri triangoli.    

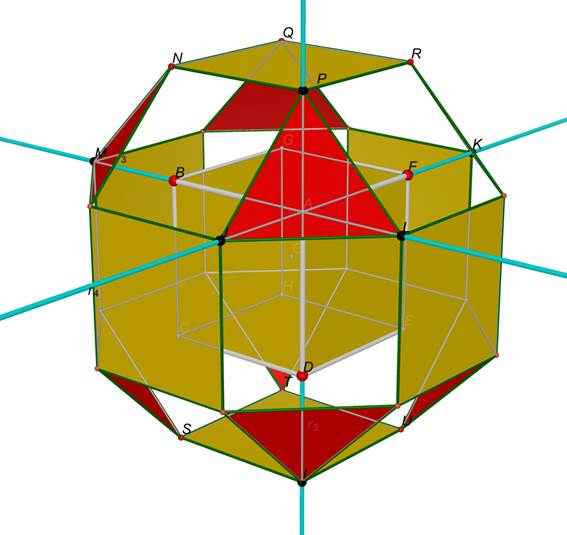
Figura 8

 

 Disegniamo con il comando “poligono” gli altri quadrilateri. 

 

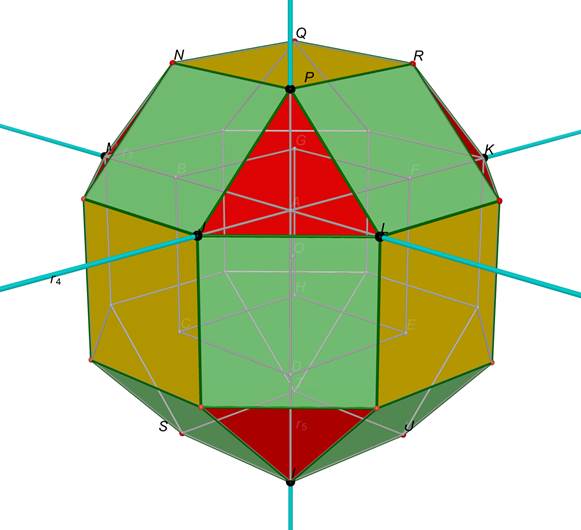
Figura 9

 

 

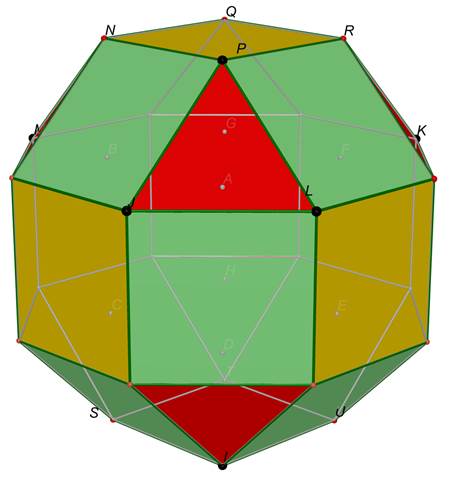
·         Abbiamo ottenuto in questo modo un’espansione del cubo.

·         Per motivi estetici nascondiamo con il comando "mostra/nascosto" le rette r3, r4 e r5 ed il punto O.

·         Nascondiamo anche le facce del cubo interno.

·         Usando il tasto destro, si può anche vedere la figura da un altro punto di vista.

 

Figura 10

 

 Utilizzando il Plug-in di Cabri 3D possiamo cliccare sulla figura 10. Trascinando il punto P si può vedere come varia il poliedro espanso al variare del punto P.

Clicca qui per accedere al file Cabri 3D con la costruzione del poliedro modificabile.

 

Dimostriamo che il poliedro costruito è archimedeo.

Per fare ciò dobbiamo dimostrare che le facce sono tutte poligoni regolari.

Le facce gialle sono, per costruzione, uguali alle facce del cubo originario. Sono quindi tutti quadrati uguali.

Consideriamo ora i triangoli. Vogliamo dimostrare che tutti i triangoli sono equilateri e che sono tutti uguali.

 

Consideriamo il triangolo PJL i cui vertici sono ottenuti per espansione dal vertice A del cubo di partenza. Quindi le distanze dei tre vertici dal punto A sono uguali e chiamiamo x questa distanza.

Abbiamo quindi

E quindi il triangolo PJL è equilatero.

Ed essendo x la distanza dei vertici degli altri triangoli dai corrispettivi vertici di partenza del cubo possiamo dire che tutti i triangoli sono equilateri e sono uguali tra loro.

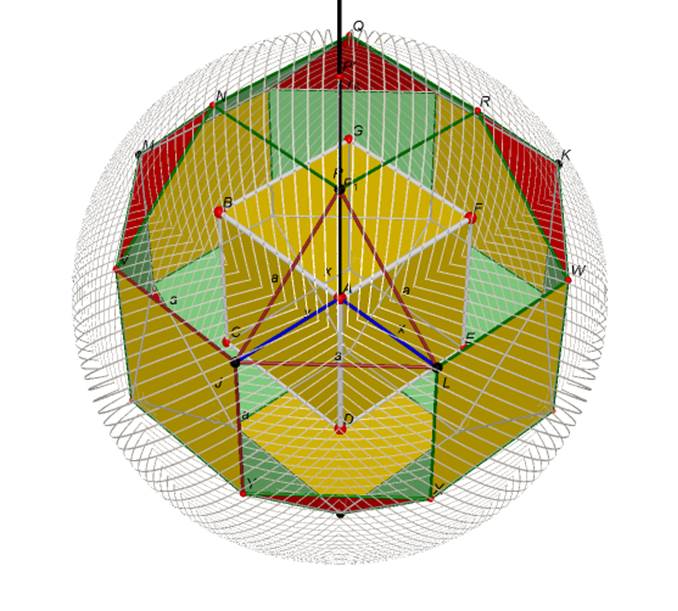
Vogliamo ora dimostrare che il quadrilatero PRWE è un rettangolo.

Per dimostrare ciò è utile visualizzare ciò che si trova all’interno del poliedro.  Vogliamo allora rendere trasparenti il triangolo PLJ e i quadrati PNQR, PRWL, PNVJ e JLXY. Facciamo ciò usando il comando "stile della superficie” e scegliendo lo stile “vuoto”. Per dimostrare che l’angolo LPR è retto bisogna considerare la retta PR, che per costruzione è parallela alla retta AF e quindi è perpendicolare al piano p contenente la faccia del cubo A B C D.

I punti P e L per costruzione appartengono al piano p. Quindi la retta PR è perpendicolare alla retta PL.  In modo analogo si dimostra che la retta WL è perpendicolare alla retta PL, che la retta PR è perpendicolare alla retta RW e che la retta LW è perpendicolare alla retta RW.

Quindi il quadrilatero PRWL è un rettangolo.  I suoi lati PR e LW hanno misura pari a l. I lati PL e RW hanno misura  e quindi si ha .

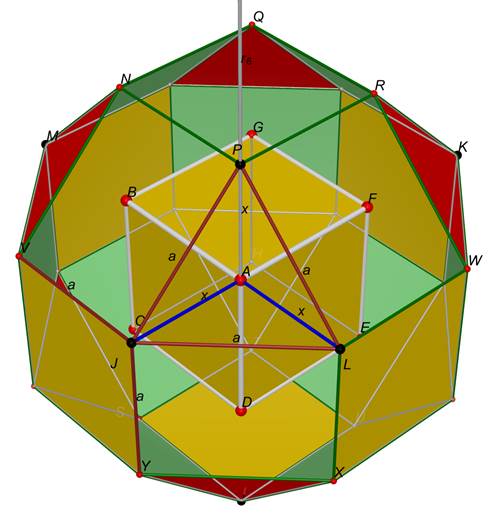
Figura 11

 

Per ottenere un poliedro archimedeo bisogna fare in modo che il rettangolo PRWL sia un quadrato Per avere un quadrato dobbiamo quindi avere   e quindi .

Osserviamo che il segmento AG misura  Consideriamo allora il punto P’, punto medio del segmento AG e la sfera di centro A e passante per P’.

Indichiamo con P1 l’intersezione di quest’ultima sfera con la semiretta s. Il punto P1 ha distanza da A uguale a    .

 

Figura 12  

Chi è dotato del Plug-in di Cabri 3D può cliccare sulla figura precedente. Trascinando il punto P di colore rosso può vedere come varia l’espansione del poliedro al variare del punto P.

Clicca qui per accedere al file Cabri 3D con la dimostrazione del poliedro modificabile.

 

             Ponendo il punto P nel punto P1 si ottiene quindi questo poliedro archimedeo.

 

Figura 13

Chi è dotato del Plug-in di Cabri 3D può cliccare sulla figura precedente. Trascinando il punto P di colore rosso può vedere come nel punto P1 la figura diventa il poliedro archimedeo rombicubottaedro.

Clicca qui per accedere al file Cabri 3D con la dimostrazione del poliedro modificabile.