






Siano  e
e  funzione test. Si ha
funzione test. Si ha

e quindi

 .
.
Mediante il cambiamento di variabile

si ottiene la relazione

ove con << >> si è indicata la dualità
in due variabili. La relazione (*) suggerisce quindi la seguente
definizione di convoluzione per due distribuzioni
 .
.
Notiamo che nelle due variabili  la funzione
la funzione  non ha supporto
limitato; infatti posto supp
non ha supporto
limitato; infatti posto supp  ,
nel piano
,
nel piano  supp
supp  è nella striscia
è nella striscia  rappresentata nella figura:
rappresentata nella figura:

Poiché la distribuzione in due variabili  è - a priori - solo sulle funzioni test in due variabili,
occorrono delle ipotesi su T ed S in modo che, di fatto, intervenga
nella dualità solo una parte limitata del supporto di
è - a priori - solo sulle funzioni test in due variabili,
occorrono delle ipotesi su T ed S in modo che, di fatto, intervenga
nella dualità solo una parte limitata del supporto di  .
I due casi principali che si considerano sono:
.
I due casi principali che si considerano sono:
- T (oppure S ) con supporto limitato. Infatti se supp
 si ha:
si ha: 
- T e S con supporto in una stessa semiretta ad esempio
 .
.
Infatti in tal caso:

implicano, di fatto, nel
triangolo di vertici (0,0), (0,b), (b,0) del I quadrante (supposto
b > 0).
nel
triangolo di vertici (0,0), (0,b), (b,0) del I quadrante (supposto
b > 0).
Per ogni distribuzione T è possibile considerare la convoluzione
con la  di Dirac
di Dirac  e si ha
e si ha

ossia
 .
.
La  si comporta come l'unità
del prodotto di convoluzione. Non è invece possibile, ad
esempio, considerare la convoluzione
si comporta come l'unità
del prodotto di convoluzione. Non è invece possibile, ad
esempio, considerare la convoluzione 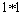 . Infatti essendo supp
1 = R, segue che
. Infatti essendo supp
1 = R, segue che 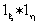 ha supporto su tutto il piano.
ha supporto su tutto il piano.













 e
e  funzione test. Si ha
funzione test. Si ha





 .
.








 si ha:
si ha: 
 .
.







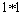 . Infatti essendo supp
1 = R, segue che
. Infatti essendo supp
1 = R, segue che 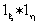 ha supporto su tutto il piano.
ha supporto su tutto il piano.