DOMANDA

Una sfera è illuminata da una lampadina (che immaginiamo puntiforme). Che curva è la linea di confine tra la parte illuminata e quella in ombra? Perché?

VERSO LA RISPOSTA

Facciamo alcuni esperimenti.

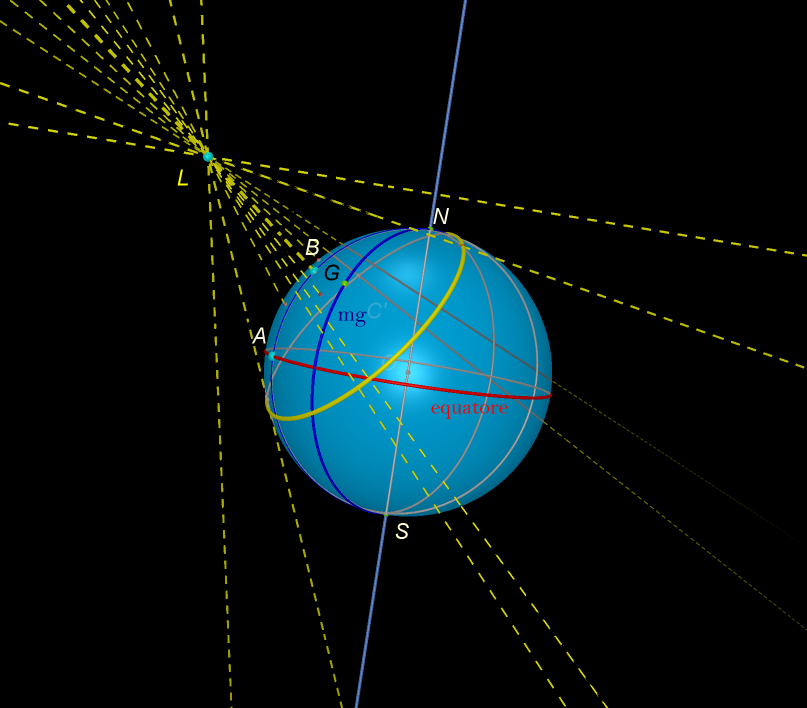
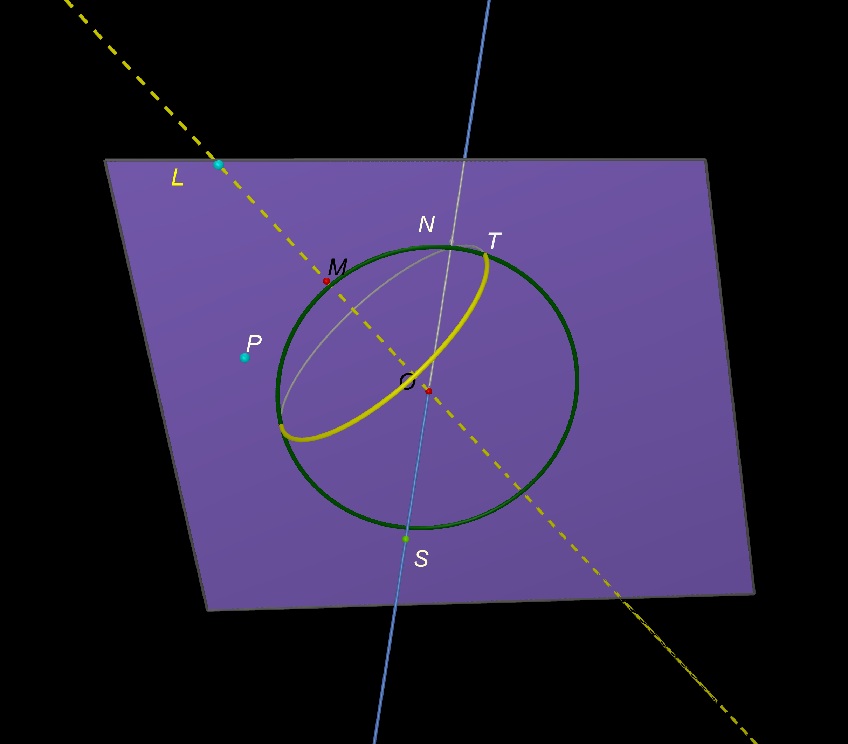
Ecco un modello creato con Cabri3D. In esso abbiamo evidenziato:

- due punti N e S diametralmente opposti (per ricordare il polo Nord e polo sud della terra)

- un cerchio massimo mg passante per N e S (per ricordare il meridiano di Greenwich)

- “ l’equatore”, cioè il cerchio massimo perpendicolare alla retta per N e S.

- Il punto luce L

- alcuni raggi luce (le rette tratteggiate in giallo)

- il confine luce-ombra (linea gialla).

Cliccando sull’immagine si può allontanare (o avvicinare) dalla sfera la lampadina L e spostare la posizione della lampadina muovendo i punti A e B.

La linea gialla di confine luce-ombra è una circonferenza.

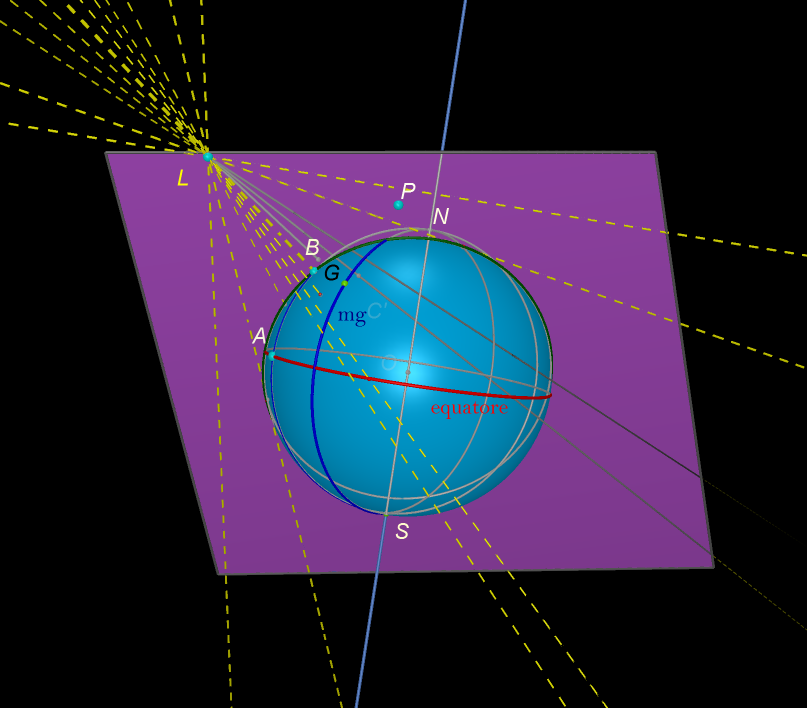
Su quale piano giace? Quale è il suo centro?

Per rispondere a questa domanda consideriamo un punto P dello spazio e poi consideriamo il piano (in viola nella figura) passante per P, L e il centro O della sfera.

Cliccando sulla figura puoi spostare la posizione della lampadina L (muovendo A, B e L) e far ruotare il piano muovendo P.

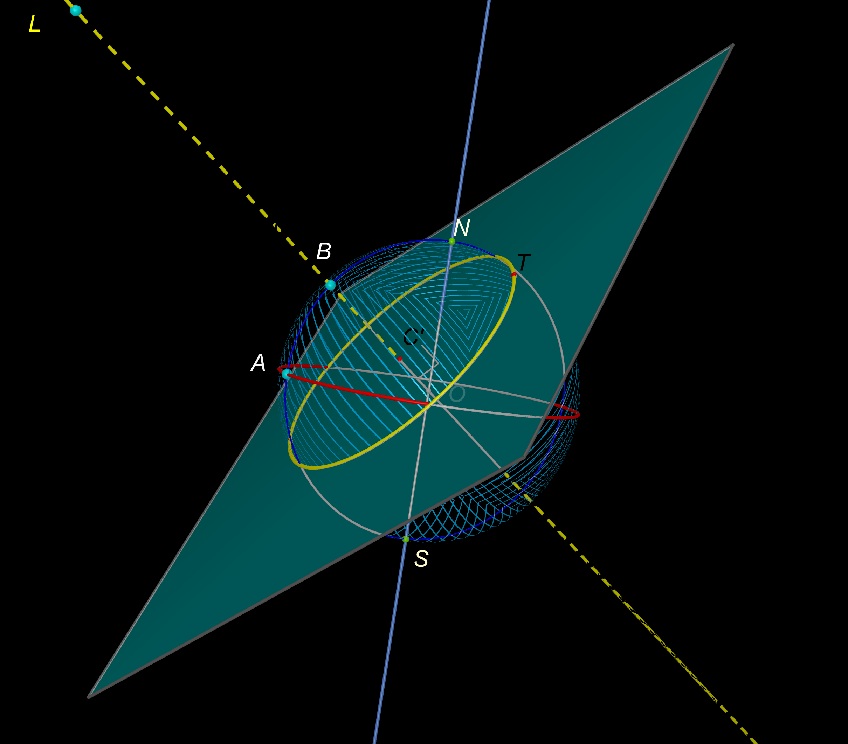
Il piano interseca la sfera in una circonferenza (verde nella figura).

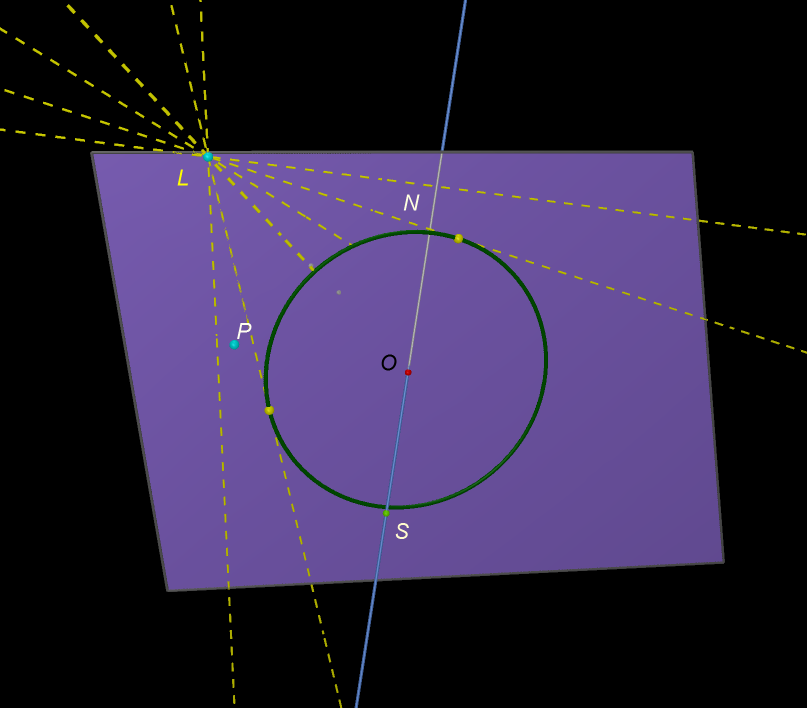
Concentriamo l’attenzione sul piano.

Alcuni raggi non toccano la circonferenza, due raggi sono tangenti alla circonferenza.

Cliccando sulla figura puoi spostare la lampadina muovendo L e puoi far ruotare il piano muovendo P.

Vogliamo determinare i punti di tangenza.

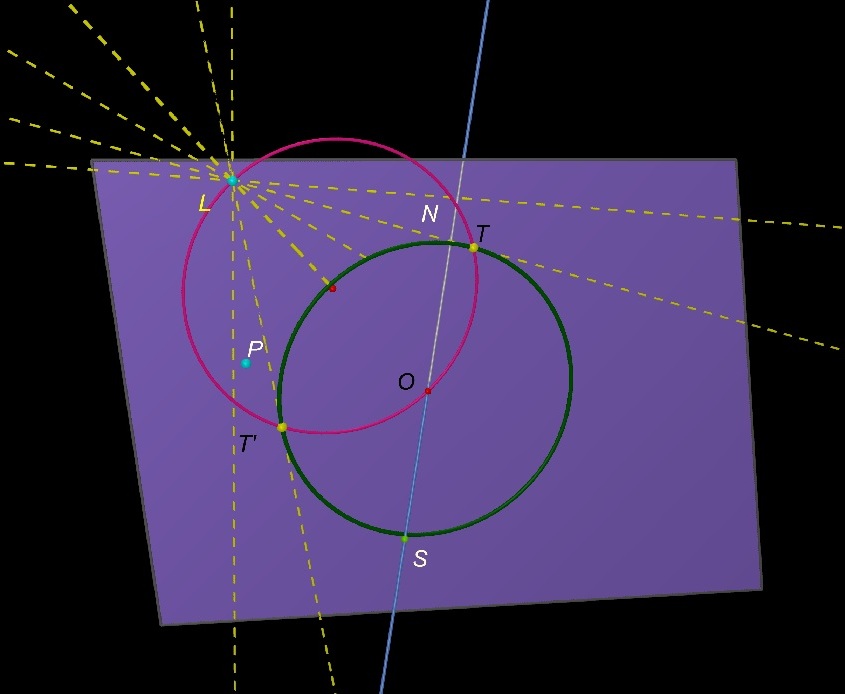
Una retta tangente ad una circonferenza è perpendicolare alla retta passante per il punto di tangenza T e per il centro della circonferenza.

Un punto di tangenza T deve quindi essere tale che l’angolo LTO sia retto.

Deve quindi appartenere alla circonferenza avente come diametro OL.

E quindi i punti di tangenza sono i due punti di intersezione della circonferenza verde con la circonferenza rossa.

Cliccando sulla figura puoi spostare la lampadina muovendo L e puoi far ruotare il piano muovendo P.

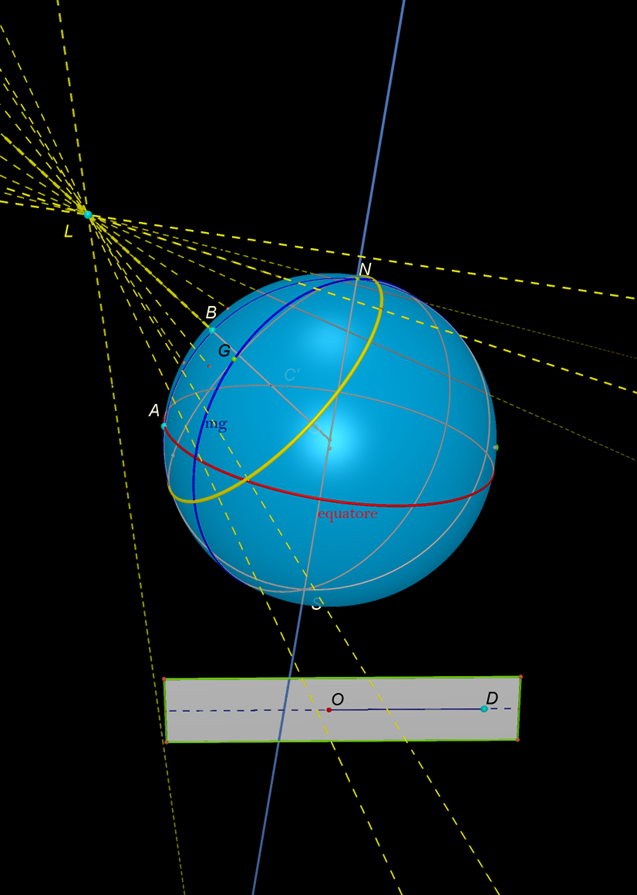
I punti di tangenza dividono la circonferenza verde in due archi. Uno ha tutti i punti illuminati, l’altro ha tutti i punti in ombra.

Gli estremi dell’arco appartengono quindi alla linea di confine luce-ombra sulla sfera.

Se ora ruotiamo il piano viola intorno alla retta OL, uno dei due punti di tangenza descrive una circonferenza.

Cliccando sulla figura puoi spostare la lampadina muovendo L e puoi far ruotare il piano muovendo P.

La circonferenza è contenuta nel piano passante per il punto di tangenza T perpendicolare alla retta passante per O e L.

Il centro è nell’intersezione di questo piano con la retta passante per O e L.

La linea di confine luce-ombra su una sfera è la circonferenza ottenuta facendo ruotare un punto di tangenza intorno alla retta passante per il centro della sfera O e il punto luce L.

Quindi appartiene ad un piano perpendicolare a tale retta ed ha il centro su tale retta e su tale piano.

Cliccando sulla figura puoi spostare la lampadina muovendo A, B e L.

Nella seguente figura è possibile cambiare la scala del modello lampadina-sfera spostando il punto D.

Cliccando sulla figura puoi cambiare la scala muovendo D e spostare la lampadina muovendo A, B e L.

Si può allontanare di molto la lampadina dalla sfera nel seguente modo.

Si riduce la scala, si allontana molto la lampadina, si ingrandisce di nuovo la scala. Si ottiene una figura di questo tipo:

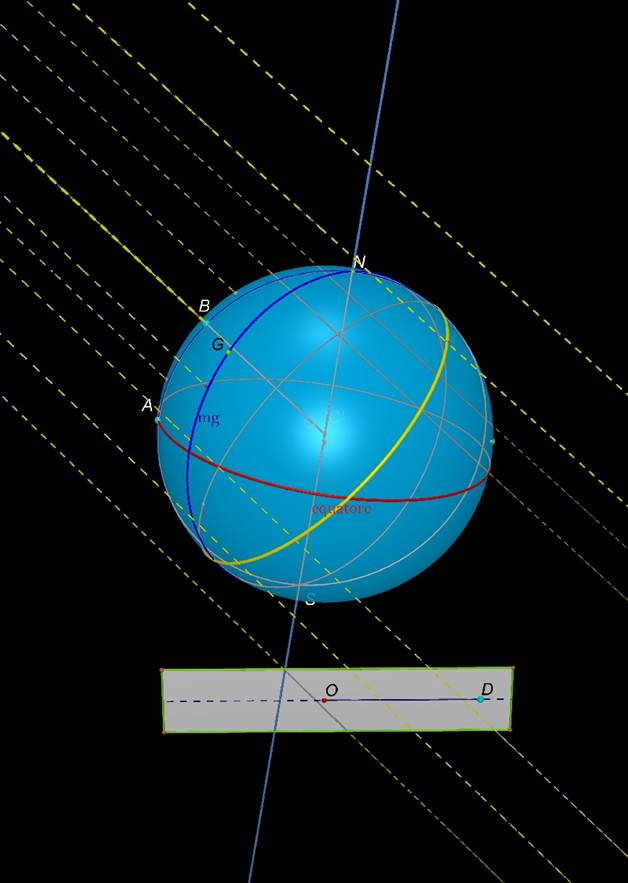
I raggi di luce appaiono paralleli.

La figura sembra rappresentare la terra e i raggi solari.

In effetti, se immaginiamo il sole come un punto, i raggi solari non sono paralleli.

Appaiono paralleli perché il sole è distante dalla terra.

RISPOSTA

La linea di confine luce-ombra è una circonferenza che giace su un piano perpendicolare alla retta congiungente la lampadina con il centro della sfera.

All’allontanarsi della lampadina dalla sfera, il centro della circonferenza si avvicina al centro della sfera.