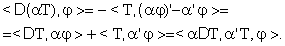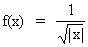si ha 
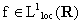e quindi essa definisce
una distribuzione, ma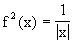 
non è localmente sommabile in R e quindi non definisce
una distribuzione. Più "irregolare" è
T e più "regolare" deve essere S affinché
il prodotto abbia significato.
Il caso più semplice è il prodotto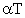 
con T in D ' (distribuzione)
e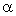 
in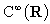 
.
Ad esempio se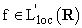 
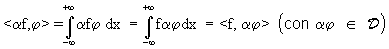
In generale ciò suggerisce la seguente definizione:
12.1 Definizione. Se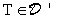 
è
una arbitraria distribuzione,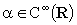 
una funzione infinitamente derivabile (in senso ordinario) allora
il prodotto 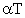si definisce
come:
.
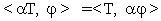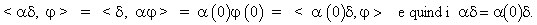In particolare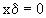 
12.3 Regola di derivazione di un prodotto.
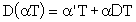.Infatti:
;
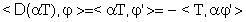essendo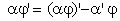 
si ha
