






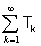 ha somma T se
ha somma T se 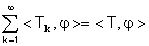 per ogni
per ogni 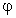 in D.
in D.
La derivazione è un operatore lineare e continuo in D' pertanto
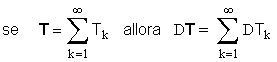 .
.
La somma della serie delle derivate 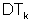 è la derivata della somma della serie delle
è la derivata della somma della serie delle 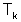 .
.
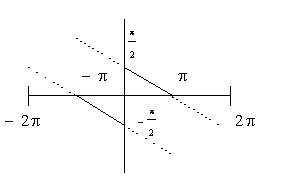
Sviluppo di Fourier della seguente funzione (dispari) periodica di periodo 2 ,
definita ponendo:
,
definita ponendo:
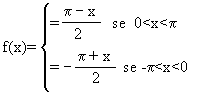
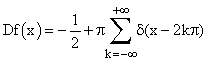 nel senso delle distribuzioni,
con
nel senso delle distribuzioni,
con
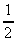 pendenza (derivata
ordinaria)
pendenza (derivata
ordinaria)
 altezza del salto
delle discontinuità
altezza del salto
delle discontinuità
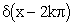 impulso (derivata
nel senso delle distribuzioni nei punti di salto).
impulso (derivata
nel senso delle distribuzioni nei punti di salto).
Scriviamo la serie di Fourier:
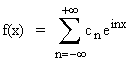
dove:
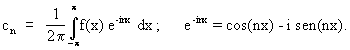
Essendo f dispari è 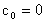 , se
, se
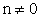 si ha:
si ha:
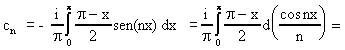
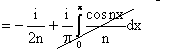
quindi:
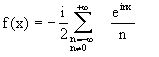
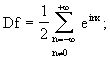
pertanto uguagliando la serie derivata alla derivata della somma:
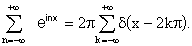
Vedremo le conseguenze di queste identità (nel senso delle distribuzioni) quando si effettua la trasformata di Fourier del treno di impulsi.