






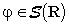 se e solo se valgono le seguenti due condizioni:
se e solo se valgono le seguenti due condizioni:
a) 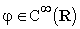 ,
,
b) per ogni coppia di interi n,m esiste una costante 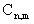 che
maggiora in modulo il momento n-imo della derivata
m-ima, cioè
che
maggiora in modulo il momento n-imo della derivata
m-ima, cioè 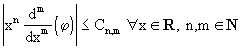
18.2 Proposizione. Tutti i momenti di tutte le derivate
di 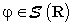 sono funzioni
sommabili in R.
sono funzioni
sommabili in R.
Dimostrazione.
In ogni intervallo limitato [-R, R] sono sommabili perché continue; all' infinito, essendo
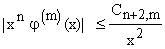
risultano sommabili per il criterio dell'infinitesimo.
18.3 Proposizione. Lo spazio S(R) è stabile sotto trasformata di Fourier.
Dimostrazione.
Posto
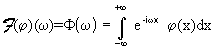
ricordiamo che (per derivazione sotto il segno di integrale) si ha:
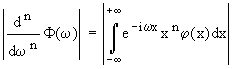
e (per integrazioni, per parti, successive)
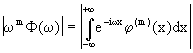
Consideriamo ora la trasformata di Fourier di 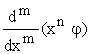 che, in quanto combinazione di momenti di derivate, è certamente
una funzione sommabile, posto:
che, in quanto combinazione di momenti di derivate, è certamente
una funzione sommabile, posto:
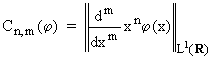
risulta 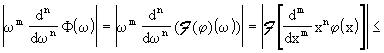
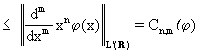
Pertanto 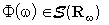 , cioè
, cioè
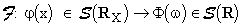 .
.
Per dimostrare che di fatto F è una trasformazione biunivoca basta osservare che la stessa proprietà vale (ovviamente) anche per F-1 ossia:
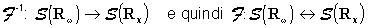
cioè F è surgettiva e iniettiva in S.