20. Esempi di Trasformate di Fourier in S'.

20.1 Esempio. Trasformata di Fourier di 1.

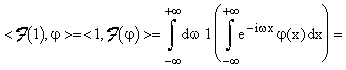
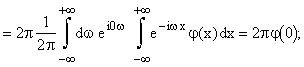
per le formule dell'antitrasformata.

Pertanto

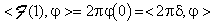
ossia .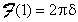

20.2 Esempio.

Trasformata di Fourier di e^ix.

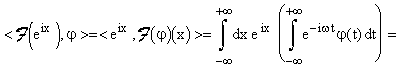
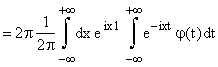
cioè:

20.3 Esempio.

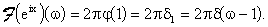
Trasformata di Fourier di .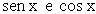
Essendo 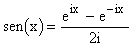, 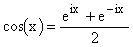. Si ha

20.4 Esempio.

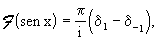
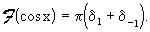
Trasformata di Fourier di una distribuzione a supporto compatto.

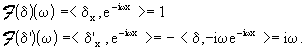
Per le distribuzioni a supporto compatto la trasformata di Fourier si può calcolare con applicazione diretta sul nucleo .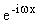

20.5 Esempio.

Trasformata di Fourier del segno di x.

avendo posto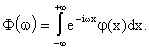

Ne segue

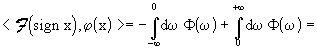
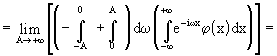
scambiando gli integrali

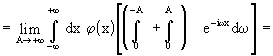
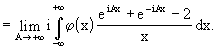
Decomponendo la funzione test nella sua parte pari (x) e nella sua parte dispari 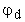(x) si ha:

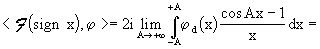
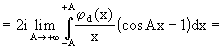
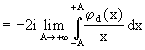per il Lemma di Riemann-Lebesgue.

Pertanto:

20.6 Esempio.

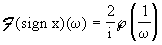
Trasformata di Fourier del gradino matematico.

Poiché per il gradino matematico si ha:

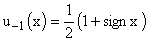
risulta:

.

20.7 Esempio.

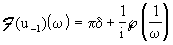Trasformata di Fourier del treno di impulsi.

(cfr. es. 11.2 Serie di distribuzioni).

E' stato dimostrata, nel senso delle distribuzioni, l'uguaglianza:

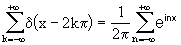
per trasformazione di Fourier ne segue:

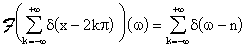
cioè un treno di impulsi si trasforma in un treno di impulsi.

20.8 Esempio.

Trasformata di Fourier di una funzione periodica.

Sia f(x) una funzione periodica di periodo 2 sviluppabile in senso di Fourier:

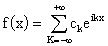
ove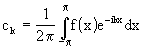

allora:

.
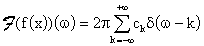