Precisamente dato un punto x noi conosciamo la funzione tramite il
suo valore assunto in x (aspetto puntuale):
.
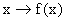Ora supponiamo di avere una famiglia di funzioni test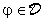 
(R)
tale che dagli integrali
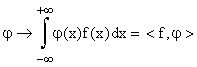
sia possibile individuare la funzione f(x) (aspetto globale).
Anche in questo modo resta definita la funzione f(x) ma inoltre si potranno definire le "funzioni generalizzate" (impulso matematico, dipolo, ecc.).
Anticipiamo per esempio l'impulso matematico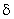 
di Dirac, che si
definisce come:
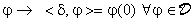
dove la dualità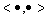 
sostituisce l'integrale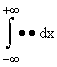 
(prodotto scalare di funzioni).
L'impulso matematico non ha significato puntuale, ma solo quando viene applicato alle funzioni test.
E' quindi fondamentale introdurre uno spazio di funzioni test
per definire le distribuzioni o funzioni generalizzate.