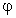appartiene a D se e
solo se è infinitamente derivabile (
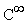(R)) ed esiste un intervallo limitato I al
di fuori del quale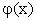 
è
zero, cioè esiste un intorno dell'infinito nei cui punti
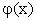è zero.
Ovviamente I non è lo stesso per ogni funzio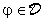ne 
.
Per ciascuna funzione ,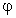
se K è il più piccolo insieme chiuso
al di fuori del quale 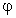è zero,
K prende il nome di supporto di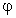
cioè:
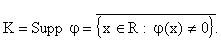
3.2 Esempio.
Sia 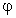definita
ponendo
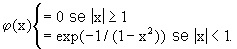
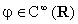a supporto 
.
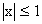Lo spazio D delle funzioni test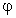
deve essere abbastanza "grande" per poter individuare
le funzioni "ordinarie" f(x) dagli integrali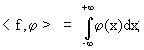 
ma anche abbastanza "piccolo" in modo che non sia troppo
restrittiva la richiesta, per le distribuzioni T, di essere definite
per ogni 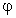, cioè
aver significato:
.
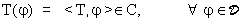Nel seguito per lo studio della trasformata di Fourier, sarà
utile considerare uno spazio di funzioni test S(R)
più grande di D
ma sempre di funzioni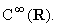 
Notiamo i seguenti risultati.
3.3 Lemma (Per funzioni continue). Se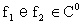 
(R)
ed inoltre: 
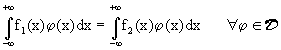allora 
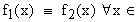R.
3.4 Lemma (Per funzioni localmente sommabili).
Se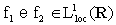 
ed inoltre: 
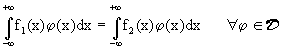allora: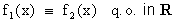 
(cioè coincidono in R a meno di un insieme di
misura nulla).
Nota: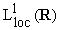 
è lo
spazio delle funzioni sommabili sui compatti di R.