Sia f una funzione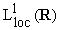 
(localmente
sommabile cioè sommabile su ogni insieme limitato) essa
definisce una distribuzione Tf nel modo seguente:
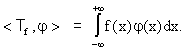
L'integrale esiste perché il dominio di integrazione di
fatto è il supporto di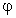 
non
tutto R. Abbiamo già visto che:
4.2 Teorema. Se due funzioni
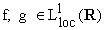definiscono la stessa distribuzione,
allora: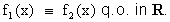 
Questo teorema permette di identificare f con Tf e scrivere
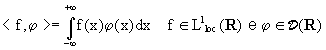
In particolare:
.
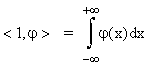La distribuzione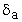 
impulso
nel punto a è così definita:
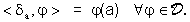
Come vedremo in seguito 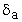non può avere una definizione puntuale
(i fisici la definiscono come la funzione sempre nulla che vale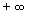 
nel punto a ed il cui integrale è 1), ma può
essere considerata il limite, nel senso della teoria delle distribuzioni,
di successioni di funzioni.
Consideriamo la successione (generalizzata):
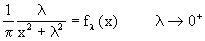
(si ottiene una successione
ponendo, ad esempio,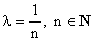 
).
Si ha
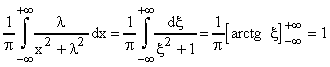
(avendo posto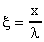
cioè
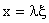). Se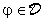 
= 
.
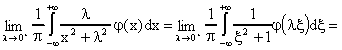
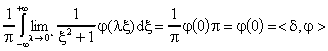Il passaggio al limite si può fare sotto il segno di integrale
per il teorema di Lebesgue (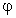è
infatti limitata).
Se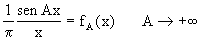 
risulta come è noto
.
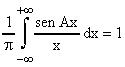S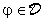e e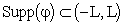 
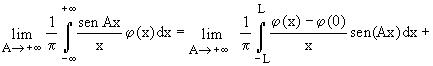
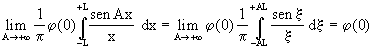
(avendo posto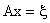 
).
Il primo integrale converge a zero per il lemma di Riemann-Lebesgue, essendo
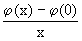regolare anche in x = 0.