






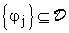 converge
ad una funzione
converge
ad una funzione 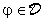 se:
se:
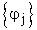 sono contenuti in uno stesso insieme limitato;
sono contenuti in uno stesso insieme limitato;
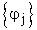 convergono uniformemente alla corrispondente derivata di
convergono uniformemente alla corrispondente derivata di 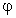 .
.
Nota: La convergenza si suppone uniforme separatamente per ogni ordine di derivate.
La definizione di convergenza si estende alle successioni generalizzate.
5.1 Definizione. Una distribuzione è un funzionale
lineare e continuo sullo spazio 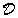 .
.
Cioè presa una distribuzione T, e posto 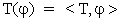 si
ha:
si
ha:
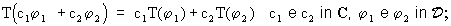
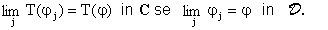
Le distribuzioni formano uno spazio vettoriale che indicheremo con D' ed in cui la somma è definita da:
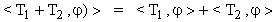
ed il prodotto per un numero complesso da:
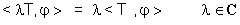
(Lo spazio delle distribuzioni D' è lo spazio duale di D).